第46話 新型インフルエンザの感染者数の推移(六一学者の千字一話)


六一学者 - 吉澤 正氏
(第10回JUSEパッケージ活用事例シンポジウムにて)
2009年4月以来,メキシコからはじまって,当初は豚インフルエンザといわれた新型インフルエンザがアメリカ,カナダ,そして世界へと急速に伝染した.5月の初旬,連休の頃に,世界での感染者数の一日ごとの発表数が,約200人,300人,500人,800人と増加した様子を見て,筆者は,次の日は1300人,その次は2100人になるかなと予想した.
フィボナッチ数列か?
これは,フィボナッチ数列を思い出したからである.
フィボナッチ数列は,前日と前々日の合計がその日の数値となる数列で,イタリアの数学者が兎の増加のモデルとして考えたといわれる.ある月に生まれたつがいのウサギは2月後には成長して1つがいのウサギを生み,それからは毎月1つがいのウサギを生み続けるという仮定をおいた.
感染者の場合,新しい感染者は2日後から毎日感染者を生み出すということに相当する.このモデルが当てはまると,大変な勢いで感染者が増えることになり,ひと月も経つと,いわゆる黄金比の約1.618倍の比率で増加することになる.
ちなみに,200人,300人から始めると,500, 800, 1300, 2100, 3400, 5500, 8900, 14400と10日で14400人になり,20日後には177万人,30日後には2億2千万人ほどになる.実際は,感染者の伝染力は急速に衰えるので,そうはならない.
日々のデータをプロット
| 曜日 | 曜日 | 感染者数 | 1日増加率 |
|---|---|---|---|
| 木 | 4月30日 | 259 | − |
| 金 | 5月1日 | 480 | 1.853 |
| 土 | 5月2日 | 575 | 1.198 |
| 日 | 5月3日 | 802 | 1.395 |
| 月 | 5月4日 | 903 | 1.126 |
| 火 | 5月5日 | 1206 | 1.336 |
| 水 | 5月6日 | 1542 | 1.279 |
| 木 | 5月7日 | 2120 | 1.375 |
| 金 | 5月8日 | 2471 | 1.166 |
| 土 | 5月9日 | 3402 | 1.377 |
| 日 | 5月10日 | 4342 | 1.276 |
| 月 | 5月11日 | 4403 | 1.014 |
| 火 | 5月12日 | 5223 | 1.186 |
| 水 | 5月13日 | 5907 | 1.131 |
| 木 | 5月14日 | 6464 | 1.094 |
| 金 | 5月15日 | 7672 | 1.187 |
| 土 | 5月16日 | 8401 | 1.095 |
| 日 | 5月17日 | 8477 | 1.009 |
| 月 | 5月18日 | 8793 | 1.037 |
| 火 | 5月19日 | 9824 | 1.117 |
| 水 | 5月20日 | 10218 | 1.040 |
| 木 | 5月21日 | 10652 | 1.042 |
| 金 | 5月22日 | 11148 | 1.047 |
| 土 | 5月23日 | 12139 | 1.089 |
| 日 | 5月24日 | 12462 | 1.027 |
| 月 | 5月25日 | 12526 | 1.005 |
| 火 | 5月26日 | 12803 | 1.022 |
| 水 | 5月27日 | 13423 | 1.048 |
| 木 | 5月28日 | 14935 | 1.113 |
| 金 | 5月29日 | 15459 | 1.035 |
| 土 | 5月30日 | 16774 | 1.085 |
| 日 | 5月31日 | 17218 | 1.026 |
| 月 | 6月1日 | 17376 | 1.009 |
| 火 | 6月2日 | 18673 | 1.075 |
| 水 | 6月3日 | 19472 | 1.043 |
| 木 | 6月4日 | 20000 | 1.027 |
そこで,正確なデータを知りたいと思ったが,5月の初めから日本経済新聞は,世界地図の上に各国で確認された感染者数(アメリカの場合は感染が濃厚とされる患者を含む)を発信していることに気が付いた.朝刊の情報は,日本時間午前0時や1時ごろの集計値で,夕刊には昼ごろのデータが記載されていた.
これも5月20日まででその後は,地図上ではなく一覧表形式になり,25日ぐらいからはそれも記載されなくなった.その後は,ネット上で共同通信などの配信データを調べた.
なお,世界保健機構 (WHO) では,世界で確認された感染者と死者の人数をほぼ毎日(ときには2日おいて)公表している.ここでは,4月30日からの朝のデータを表1に示しておこう.表1には,毎日の増加率も示してある.
推移をグラフで見る
表1の感染者と毎日の増加率を折れ線グラフにしたのが図1である.図1の左軸が感染者数,右軸が増加率である.
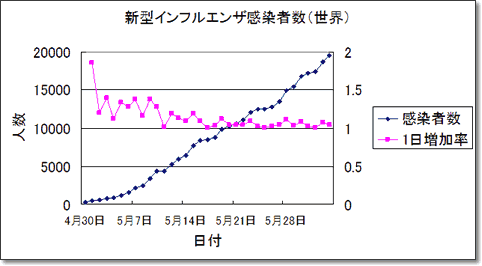
図1 新型インフルエンザ感染者数
(試験所で確認されたもの,米国は感染が濃厚と判断された者を含む)
5月20日に1万人を超え,6月4日に2万人を超えた.ただし,6月4日の正確な数字はいつもの時間には見つからなかった.6月3日の時点で,70の国・地域に広がり,死者数は5カ国で124人.日本での感染者数は400人を超えた.
このように単調に増加して行く推移は,成長型ともいわれるが,それを観察する基本は,毎日の増加率あるいは増加数の変化を見ることである.この場合,増加率でみると,最初の10日間あたりは1.3 倍ぐらいで,フィボナッチ数ほどではないが,この勢いで増加したら,20日後には6万人になってしまう.実際は,その後の伸び率は,少し衰えて,1.1程度であり,グラフ全体でみれば,直線的になっている.
感染者の増加現象のモデルを考えることはここでは控えておくが,ここで扱った感染者数は試験所で確認されたデータであり,試験所での検査能力に影響されることも無視できない.また,社会的あるいは経済的影響を考慮して,実際の感染者数の推定値の発表は慎重に行われていることも考える必要がある.
成長型の推移データについては,増加率が一定の指数型や増加数が一定の直線型のようにどこまでも成長していくモデルでなく,どこかで飽和状態に達することになるモデルを考えることが多い.統計ソフトのStatWorksの時系列分析では,ゴンペルツ曲線やロジスティック曲線をあてはめることができる.
このデータは,ゴンペルツ曲線の方がロジスティック曲線より当てはまりがよいが,飽和する数値の予測は,毎日データが増えるごとに結構変動する.その詳しい様子は別の機会に説明したい.なお,曜日も考えて,分析すると週末は確認される感染者数が少ないことがわかる.週末ぐらいは休まないと試験所の疲れもとれないことだろう.
2009年6月10日掲載
イベント案内や製品などの最新情報をお届けします